Saturday, 28 November 2009

Numbers, Big Numbers.




A googolplex is the number 10googol, which can also be written as the number 1 followed by a googol of zeros (i.e., 10100 zeros).
1 googolplex
= 10googol
= 10(10100)
= 1010,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

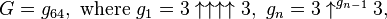
Writing it in numerals would be physically impossible, since doing so would require more space than there is in the known universe.
An average book of 60 cubic inches can be printed with 5 x 105 '0's (5 characters per word, 10 words per line, 25 lines per page, 400 pages), or 8.3 × 103 '0's per cubic inch. The observable universe contains 6 × 1083 cubic inches (1.3 × π × (14 × 109 light year in inches)3).
This implies that if the universe is stuffed with paper printed with '0's, it could contain only 5.3 × 1087 '0's, far short of a googol of '0's. In fact there are only about 2.5 × 1089 elementary particles in the observable universe so even if you could write a zero on each elementary particle, you would still have to make the universe's mass about a trillion times larger to complete the number.
The time it would take to write such a number also renders the task impossible: if a person writes two digits per second, it would take around about 1.51 × 1092 years, which is 1.1 × 1082 times the age of the universe, to write a googolplex.
That's pretty fucking big, but a bright chap called Graham has an even bigger one named after him, notated here as G. \left. \begin{matrix} G &=&3\underbrace{\uparrow \uparrow \cdots\cdots\cdots\cdots\cdots \uparrow}3 \\ & &3\underbrace{\uparrow \uparrow \cdots\cdots\cdots\cdots \uparrow}3 \\ & &\underbrace{\qquad\;\; \vdots \qquad\;\;} \\ & &3\underbrace{\uparrow \uparrow \cdots\cdot\cdot \uparrow}3 \\ & &3\uparrow \uparrow \uparrow \uparrow3 \end{matrix} \right \} \text{64 layers}
The number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,
G = g_{64},\text{ where }g_1=3\uparrow\uparrow\uparrow\uparrow 3,\ g_n = 3\uparrow^{g_{n-1}}3,
G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3's; the second step is to calculate g2 with g1 up-arrows between 3's; the third step is to calculate g3 with g2 up-arrows between 3's; and so on, until finally calculating G = g64 with g63 up-arrows between 3's.
g_1 = 3 \uparrow \uparrow \uparrow \uparrow 3 = 3 \uparrow \uparrow \uparrow (3 \uparrow \uparrow \uparrow 3) = 3 \uparrow\uparrow (3 \uparrow\uparrow (3 \uparrow\uparrow \ \dots \ (3 \uparrow\uparrow 3) \dots ))
(3^^^3 = 3^^(3^^3) is 3^^7,625,597,484,987 = 3^(7,625,597,484,987^7,625,597,484,987), which makes a tower of exponents 7,625,597,484,987 layers high.)
Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volumes (roughly 10^185 of them) into which one can imagine subdividing the observable universe. And after this first term, there are still another 63 terms in the g sequence before Graham's number G = g64 is reached.
That's really fucking big, but size isn't everything. It's not perfect, unlike these few examples of the Perfect Number, starting with our humble 6 (no-one knows how many more there are):

6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128,2658455991569831744654692615953842176,191561942608236107294793378084303638130997321548169216,13164036458569648337239753460458722910223472318386943117783728128,14474011154664524427946373126085988481573677491474835889066354349131199152128,23562723457267347065789548996709904988477547858392600710143027597506337283178622239730365539602600561360255566462503270175052892578043215543382498428777152427010394496918664028644534128033831439790236838624033171435922356643219703101720713163527487298747400647801939587165936401087419375649057918549492160555646976,141053783706712069063207958086063189881486743514715667838838675999954867742652380114104193329037690251561950568709829327164087724366370087116731268159313652487450652439805877296207297446723295166658228846926807786652870188920867879451478364569313922060370695064736073572378695176473055266826253284886383715072974324463835300053138429460296575143368065570759537328128, 54162526284365847412654465374391316140856490539031695784603920818387206994158534859198999921056719921919057390080263646159280013827605439746262788903057303445505827028395139475207769044924431494861729435113126280837904930462740681717960465867348720992572190569465545299629919823431031092624244463547789635441481391719816441605586788092147886677321398756661624714551726964302217554281784254817319611951659855553573937788923405146222324506715979193757372820860878214322052227584537552897476256179395176624426314480313446935085203657584798247536021172880403783048602873621259313789994900336673941503747224966984028240806042108690077670395259231894666273615212775603535764707952250173858305171028603021234896647851363949928904973292145107505979911456221519899345764984291328.

And then, of course, you've got infinity a.k.a. Aleph Null. Sort of.
It can't be annotated but Albert Einstein, who knew a thing or two about numbers, said
"Only two things are infinite, the Universe and human stupidity, and I'm not sure about the former." 











Posted by



at











































1 comment:































        

      









Subscribe to:
Post Comments (Atom)